CENTRO DE GRAVEDAD
CONCEPTO
Es aquel punto
geométrico ubicado dentro o fuera de un cuerpo, por el cual pasa la línea de
acción de la fuerza resultante de las fuerzas de gravedad que actúan sobre cada
una de las partículas que forman el cuerpo.
1. Peso (W) es una magnitud vectorial. Viene a
ser la fuerza resultante que ejerce la tierra sobre los cuerpos que lo rodean.
Se representa por un vector que indica el centro de la tierra.
Peso
= m.g
2. El centro de gravedad (G) es considerado
como el punto donde está concentrado el peso de un cuerpo, y sobre el cual se
debe aplicar una fuerza numéricamente igual al peso para establecer el
equilibrio.
3. Cuando se sostiene un cuerpo de puntos
diferentes, como los mostrados en las figuras,
se nota que el centro de gravedad se encuentra debajo del punto de
suspensión.
Si
se prolongan las líneas de suspensión, vemos que éstas se cortan en el punto
donde se encuentra el centro de gravedad (G) del cuerpo.
4. Con el Teorema de Varignon se determina el
centro de gravedad del sistema respecto de un sistema de coordenadas, para un
cuerpo constituido por componentes cuyos centros de gravedad están
establecidos.
W
= W1 + W2 + W3
5.
Teorema de Varignon respecto del eje
“y”
W.x = W1.x1+W2.x2+W3.x3
X: Abscisa del centro de gravedad.
Teorema de Varignon respecto del eje “x”
W.y = W1.y1 + W2.y2
+ W3.y3
Y: Ordenada del centro de gravedad.
6.
Para cuerpos linealmente homogéneos como en la figura anterior, el peso se
puede escribir en función de su longitud. El peso es directamente proporcional
a su longitud.
W1=K.L1 ; W2=K.L2
; W3=K.L3
Remplazando en las ecuaciones (1) y (2), se obtienen
las siguientes ecuaciones:
7.
Para cuerpos superficialmente homogéneos (densidad constante e igual espesor),
el peso es directamente proporcional al área.
W1=K.A1 , W2=K.A2 ,
W3=K.A3
Reemplazando en las ecuaciones (1) y (2).
8.
Para un sistema de cuerpos.
Peso = Peso específico x volumen
W1=K.V1 , W2=K.V2 , W3=K.V3
Reemplazando los valores se obtienen
CENTRO DE MASA
CONCEPTO
Es aquel punto
geométrico donde se le considera la concentración de la masa de un sistema de
partículas.
Al aplicar el Teorema
de Varignon se puede hallar la posición del centro de masa respecto de un
sistema de coordenadas.
a)
La posición del centro de masas está definido por las coordenadas (x,y)
b)
Teniendo en consideración que Peso=mg
c)
Estas fórmulas se pueden generalizar para un sistema “n” partículas.
Por tanto, en términos generales:
Teniendo en cuenta que la circunferencia
es una curva plana y cerrada cuyos puntos son equidistantes
de otro ubicado en su interior el cual es llamado centro y el círculo es el área o
superficie plana que está contenida dentro de una circunferencia, entonces:
Cuarto de círculo
Semicírculo
Arco de Circunferencia
Sector Circular
Trapecio
Prisma
Cilindro
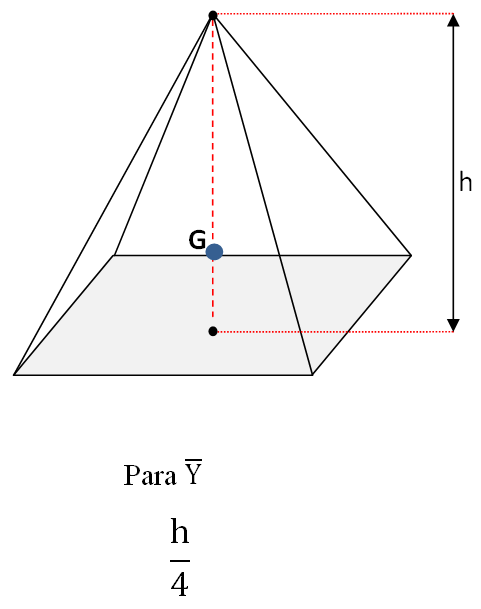
Pirámide
Cono
Hemisferio
Ejercicios ilustrativos
1.- En la figura se
muestra un cono recto de altura 40cm y radio 20cm, suspendido desde el punto P.
Si 0 es punto medio de la base y P es el
punto medio del radio, determine el ángulo “θ” que forma el eje del cono con la
vertical.
Solución
En la posición de equilibrio, el Peso (W) y la
Tensión (T) son colineales, por tanto los puntos P y G se encuentran en la
misma vertical.
Siendo OP la mitad del Radio, entonces OP= 10cm
2.- En los vértices de
un cuadrado de lados 2m se colocaron cuatro partículas. Determinar el centro de
masa respecto del sistema de coordenadas.
Solución
Tenemos que la masas m1,
m2, m3 y m4
pesan 1kg, 2kg, 3kg y 4kg respectivamente.
Entonces según la
posición r = (X ; Y) y considerando la distancia entre partícula y partícula.
r1 = (0 ; 2)
r2 = (2 ; 2)
r3 = (2; 0)
r4 = (0 ; 0)



























No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.